已知函数 (
( ),在区间
),在区间 上有最大值4,最小值1,设
上有最大值4,最小值1,设 .
.
(1)求 的值;
的值;
(2)不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
已知条件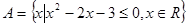 ; B=
; B=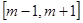 ,
,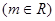
(Ⅰ)若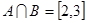 ,求实数
,求实数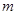 的值;
的值;
(Ⅱ)若B是A的子集,求实数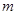 的取值范围.
的取值范围.
计算:
(14分)在直角坐标系 中椭圆
中椭圆 :
:
 的左、右焦点分别为
的左、右焦点分别为 、
、 .其中
.其中 也是抛物线
也是抛物线 :
: 的焦点,点
的焦点,点 为
为 与
与 在第一象限的交点,且
在第一象限的交点,且 .
.
(1)求 的方程;
的方程;
(2)平面上的点 满足
满足 ,直线
,直线 ∥
∥ ,且与
,且与 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
(12分)已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)= +6x的图象关于y轴对称.
+6x的图象关于y轴对称.
(1)求m、n的值及函数y=f(x)的单调区间;
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
设等比数列 的前
的前 项和为
项和为 ,已知
,已知 N
N ).
).
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.