已知某海滨浴场的海浪高度 (单位:米)与时间
(单位:米)与时间 
 (单位:时)的函数关系记作
(单位:时)的函数关系记作 ,下表是某日各时的浪高数据:
,下表是某日各时的浪高数据:
 /时 /时 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 /米 /米 |
1.5 |
1.0 |
0.5 |
1.0 |
1.5 |
1.0 |
0.5 |
0.99 |
1.5 |
经长期观测,函数 可近似地看成是函数
可近似地看成是函数 .
.
(1)根据以上数据,求出函数 的最小正周期T及函数表达 式(其中
的最小正周期T及函数表达 式(其中 );
);
(2)根据规定,当海浪高度不低于0.75米时,才对冲浪爱好者开放,请根据以上结论,判断一天内从上午7时至晚上19时之间,该浴场有多少时间可向冲浪爱好者开放?
(本小题满分12分)
已知函数: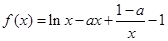
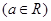 .
.
(1) 当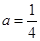 时①求
时①求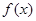 的单调区间;
的单调区间;
②设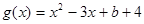 ,若对任意
,若对任意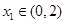 ,存在
,存在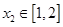 ,使
,使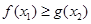 ,求实数
,求实数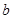 取值范围.
取值范围.
(2) 当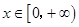 时,恒有
时,恒有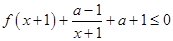 成立,求
成立,求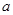 的取值范围.
的取值范围.
(本小题满分12分)
已知三点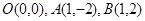 ,曲线
,曲线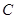 上任一点
上任一点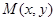 满足
满足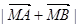 =
=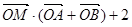
(1) 求曲线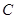 的方程;
的方程;
(2) 设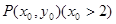 是(1)中所求曲线
是(1)中所求曲线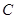 上的动点,定点
上的动点,定点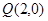 ,线段
,线段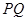 的垂直平分线与
的垂直平分线与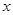 轴交于点
轴交于点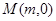 ,求实数
,求实数 的最小值.
的最小值.
(本小题满分12分)
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下(阴影部分为损坏数据),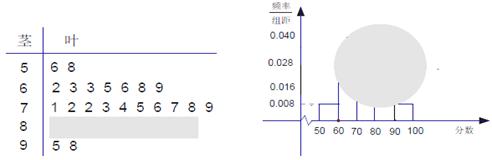
据此解答如下问题:
(1) 求本次测试成绩的中位数,并求频率分布直方图中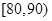 的矩形的高(用小数表示);
的矩形的高(用小数表示);
(2) 若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
(本小题满分12分)
如图,在四棱锥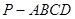 中,平面
中,平面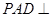 平面
平面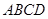 ,
,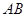 ∥
∥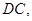
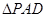 是正三角形,已知
是正三角形,已知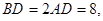
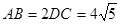
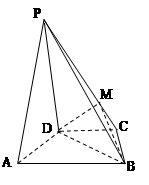
(1) 设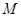 是
是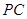 上的一点,求证:平面
上的一点,求证:平面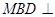 平面
平面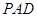 ;
;
(2) 求四棱锥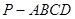 的体积.
的体积.
(本小题满分12分)
在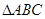 中,角
中,角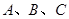 的对边分别为
的对边分别为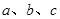 ,
,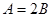 ,
,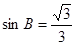 .
.
(1) 求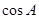 及
及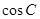 的值.
的值.
(2) 若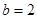 ,求
,求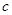 .
.