直角坐标系xOy中,有一半径为R的圆形匀强磁场区域,磁感应强度为B,磁场方向垂直xOy平面指向纸面内,该区域的圆心坐标为(R,0),有一个质量为m、带电荷量为-q的离子,以某一速度进入该磁场,不计重力;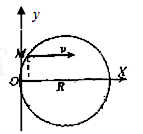
(1)若离子从O点沿x轴正方向射入,出射时相对入射方向改变了90°角,求离子速度大小;
(2)若离子从点(0,R/2)沿x轴正方向射入磁场,离子从射入磁场到射出磁场通过了该磁场的最大距离,求离子在磁场区域经历的时间。
汽车发动机的额定功率为60kw,汽车的质量为l×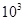 kg,汽车在水平路面上行驶时,阻力是车的重力的0.2倍,若汽车始终保持额定的功率不变,取g=
kg,汽车在水平路面上行驶时,阻力是车的重力的0.2倍,若汽车始终保持额定的功率不变,取g=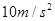 ,则从静止起动后:
,则从静止起动后:
(1)汽车做什么运动;
(2)汽车所能达到的最大速度是多少;
(3)当汽车的加速度为1m/s2时,汽车的速度是多少。
人类一直梦想登上月球,将月球作为人类的第二个家园。现根据观测已知月球的质量为M,半径为R,自转周期为T,万有引力常量为G。请你结合以上数据求下列各值:
(1)月球表面的重力加速度g月;
(2)月球的第一宇宙速度v;
(3)月球同步卫星的轨道半径r。
如图所示,将一个小球水平抛出,抛出点距水平地面的高度h=1.8m,小球抛出的初速度为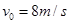 。不计空气阻力。取g=
。不计空气阻力。取g=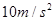 。求:
。求: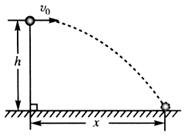
(1)小球从抛出到落地经历的时间t;
(2)小球落地点与抛出点的水平距离x;
(3)小球落地时的速度大小v。
如图所示,细绳上端固定于水平轴O,下端系一质量m=1.0kg的小球,组成一摆长为L= 0.2m的摆。摆原来处于静止状态,且小球与光滑平台的边缘接触,但对平台无压力,平台高h= 0.8m。一个质量为M= 2.0kg的滑块,以速度v0沿平台水平向右运动与小球发生正碰。碰后小球在绳的约束下运动,经四分之一个圆弧到达A点速度减为零,滑块M落在水平地面的C点,C点距平台边缘的水平距离x= 1.2m。取g=10m/s2。求:
(1)碰后滑块的速度大小v;
(2)碰后小球的速度大小vm;
(3)碰后系统损失的机械能△E。
过山车是游乐场中常见的设施。如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R= 2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点。一个质量为m=1.0kg的小滑(可视为质点),从轨道的左侧A点以v0= 12m/s的初速度沿轨道向右运动,A、B间距L= 11.5m。小滑块与水平轨道间的动摩擦因数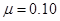 。圆形轨道是光滑的,水平轨道足够长。取重力加速度g=10m/s2。求:
。圆形轨道是光滑的,水平轨道足够长。取重力加速度g=10m/s2。求:
(1)滑块经过B点时的速度大小 ;
;
(2)滑块经过C点时受到轨道的作用力大小F;
(3)滑块最终停留点D(图中未画出)与起点A的距离d。