如图所示，在xOy平面的第一象限内，分布有沿x轴负方向的场强E=
×104N/C的匀强电场，第四象限内分布有垂直纸面向里的磁感应强度B1="0.2" T的匀强磁场，第二、三象限内分布有垂直纸面向里的磁感应强度B2的匀强磁场。在x轴上有一个垂直于y轴的平板OM，平板上开有一个小孔P，P处连接有一段长度d=lcm内径不计的准直管，管内由于静电屏蔽没有电场。y轴负方向上距O点
cm的粒子源S可以向第四象限平面内各个方向发射a粒子，假设发射的a粒子速度大小v均为2×105m/s，此时有粒子通过准直管进入电场, 打到平板和准直管管壁上的a粒子均被吸收。已知a粒子带正电，比荷为
5×l07C/kg，重力不计，求：
（1）a粒子在第四象限的磁场中运动时的轨道半径和粒子从S到达P孔的时间；
（2）除了通过准直管的a粒子外，为使其余a粒子都不能进入电场，平板OM的长度至少是多长？
（3）经过准直管进入电场中运动的a粒子，第一次到达y轴的位置与O点的距离；
（4）要使离开电场的a粒子能回到粒子源S处，磁感应强度B2应为多大？
如图所示，粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾角 α＝37°，A、B是两个质量均为 m＝1 kg的小滑块（可看做质点），C为左端附有胶泥的薄板（质量不计），D为两端分别连接 B和 C的轻质弹簧．当滑块 A置于斜面上且受到大小 F＝4 N，方向垂直斜面向下的恒力作用时，恰能向下匀速运动．现撤去 F，让滑块 A从斜面上距斜面底端 L＝1 m处由静止下滑．（g＝10 m/s2，sin37°＝0．6，cos37°＝0．8），求：
（1）滑块 A到达斜面底端时的速度大小；
（2）滑块 A与 C接触后粘连在一起，求此后两滑块和弹簧构成的系统在相互作用过程中，弹簧的最大弹性势能．
真空中足够大的两个相互平行的金属板 a和 b之间的距离为 d，两板之间的电压 Uab按图所示规律变化，其变化周期为 T。在 t＝0时刻，一
带电粒子（+q）仅在该电场的作用下，由 a板从静止开始向 b板运动，并于 t＝nT（n为自然数）时刻，恰好到达 b板．求
（1）带电粒子在匀强电场中的加速度大小为多少？
（2）若粒子在 t＝时刻才开始从 a板运动，那么粒子运动时间 nT后，它将运动到离 a板多远的地方？
用30cm的细线将质量为4×10-3㎏的带电小球P悬挂在Ｏ点下，当空中有方向为水平向右，大小为1×104N/C的匀强电场时，小球偏转37°后处在静止状态（sin37°=0.6,c
os37°=0.8，g=10m/s2）。求：
（1）分析小球的带电性质
（2）求小球的带电量
（3）求细线的拉力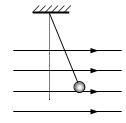
如图所示为一列简谐横波在某一时刻的波的图象，波的传播速度为5m/s，传播方向沿x正方向。求：
(1)该波的振幅、波长和周期。
(2)从图示时刻起，经过9s质点A运动的路程是多少？
(3)从图示时刻起，平衡位置位于x=22m处的质点至少再经多长时间才能到达波峰？
过山车是游乐场中常见的设施。下图是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，B、C间距与C、D间距相等，半径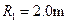
、
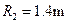。一个质量为
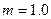kg的小球（视为质点），从轨道的左侧A点以
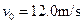的初速度沿轨道向右运动，A、B间距
m。小球与水平轨道间的动摩擦因数
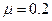，圆形轨道是光滑的。假设水平轨道足够长，圆形轨道间不相互重叠。重力加速度取
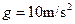，计算结果保留小数点后一位数字。试求
（1）小球在经过第一个圆形轨道的最高点时，轨道对小球作用力的大小；
（2）如果小球恰能通过第二圆形轨道，B、C间距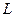
应是多少；
（3）在满足（2）的条件下，如果要使小球不能脱离轨道，在第三个圆形轨道的设计中，半径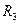
应满足的条件；小球最终停留点与起点
的距离。