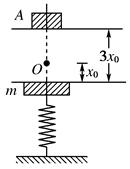
如图甲所示,粒子源能连续释放质量为m,电荷量为+q,初速度近似为零的粒子(不计重力),粒子从正极板附近射出,经两金属板间电场加速后,沿y轴射入一个边界为矩形的匀强磁场中,磁感应强度为B,磁场方向垂直纸面向里.磁场的四条边界分别是y =0,y=a,x=-1.5a,x=1.5a.两金属板间电压随时间均匀增加,如图乙所示.由于两金属板间距很小,微粒在电场中运动时间极短,可认为微粒加速运动过程中电场恒定.
(1)求微粒分别从磁场上、下边界射出时对应的电压范围;
(2)微粒从磁场左侧边界射出时,求微粒的射出速度相对进入磁场时初速度偏转角度的范围,并确定在左边界上出射范围的宽度d .
如下图所示,在绝缘的光滑水平面上有A、B两个点电荷,A带正电,B带负电,电荷量都是q,它们之间的距离为d.为使两电荷在电场力作用下都处于静止状态,必须在水平方向加一个匀强电场.求:两电荷都处于静止状态时,A、B连线的中点处场强大小和方向.(已知静电力常数为k)
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小 ,方向与x轴正方向相同.在O处放一个电荷量
,方向与x轴正方向相同.在O处放一个电荷量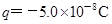 ,质量
,质量 的绝缘物块.物块与水平面间的动摩擦因数
的绝缘物块.物块与水平面间的动摩擦因数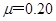 ,沿x轴正方向给物块一个初速度
,沿x轴正方向给物块一个初速度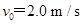 ,如上图所示.(g取
,如上图所示.(g取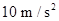 )试求:
)试求:
(1)物块向右运动的最大距离.
(2)物块最终停止的位置.
把一个电荷量为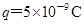 的正电荷从距电场无穷远处移到电场中M点,电荷克服电场力做功
的正电荷从距电场无穷远处移到电场中M点,电荷克服电场力做功 ,如果把该点电荷从距电场无穷远处移到电场中N点,电荷克服电场力做功
,如果把该点电荷从距电场无穷远处移到电场中N点,电荷克服电场力做功 .取无穷远处为零电势点,求:
.取无穷远处为零电势点,求:
(1)M、N点的电势是多少?
(2)M、N点的电势差是多少?把该点电荷从M点移到N点电场力做功是多少?
如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为 .但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为
.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为 .已知地球和月球的质量分别为
.已知地球和月球的质量分别为 和
和 .求
.求 与
与 两者平方之比.(结果保留3位小数)
两者平方之比.(结果保留3位小数)
质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上.平衡时,弹簧的压缩量为x0,如右图所示.一物块从钢板正上方距离为3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连.它们到达最低点后又向上运动.已知物块质量也为m时,它们恰能回到O点.若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度.求物块向上运动到达的最高点与O点的距离.