如图所示,在光滑水平面上有一辆质量M="8" kg的平板小车,车上有一个质量m="1.9" kg的木块(木块可视为质点),车与木块一起以v="1" m/s的速度水平向右匀速行驶.一颗质量m0="0.1" kg的子弹以v0="179" m/s的初速度水平向左飞,瞬间击中木块并留在其中.已知木块与平板之间的动摩擦因数 =0.54,(g="10" m/s2)求:
=0.54,(g="10" m/s2)求:
①子弹射入木块后瞬间子弹和木块的共同速度
②若是木块刚好不会从车上掉下,则小车的平板至少多长?
如图所示,有界匀强磁场的磁感应强度B=2×10-3 T;磁场右边是宽度L=0.2 m、场强E=40 V/m、方向向左的匀强电场.一带电粒子电荷量q=-3.2×10-19 C,质量m=6.4×10-27 kg,以v=4×104 m/s的速度沿OO′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出.(不计重力)求: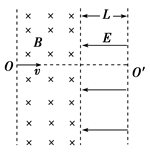
(1)大致画出带电粒子的运动轨迹;
(2)带电粒子在磁场中运动的轨道半径;
(3)带电粒子飞出电场时的动能Ek.
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d = 40cm.电源电动势E = 24V,内电阻r = 1Ω,电阻R = 15Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0 =" 4" m/s竖直向上射入板间.若小球带电量为q = 1×10-2 C,质量为m = 2×10-2 kg,不考虑空气阻力.那么,滑动变阻器接入电路的阻值为多大时,小球恰能到达A板?此时,电源的输出功率是多大?(取g ="10" m/s2)
质谱仪原理如图所示,a为粒子加速器,电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2,今有一质量为m,电量为+e的电子(不计重力),经加速后,该粒子恰能通过速度选择器,粒子进入分离器后做半径为R的匀速圆周运动.
求:(1)粒子的速度v;(2)速度选择器的电压U2; (3)粒子在磁感应强度为B2磁场中做匀速圆周运动的半径R.
如图所示,真空管内的阴极K发出的电子(不计初速、重力和电子间的相互作用)经加速电压U1加速后,穿过AA'中心的小孔沿中心轴O1 O的方向进入到两块水平正对放置的平行极板P和P'间的区域.当极板P和P'间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;若加上偏转电压U2后,亮点则偏离到O'点.已知电子带电量为-e 、质量为m,极板P和P'水平方向的长度为L、极板间距为b,极板右端到荧光屏的距离可忽略不计(如图所示) .求: 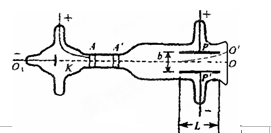
(1)打在荧光屏O点的电子速度的大小
(2)荧光屏上O'点与O点的竖直间距多大
如图所示,一质量为M的滑块静止在光滑的水平面上,其左侧是一光滑的四分之一圆弧,圆弧半径为R=1m,一质量为m的小球以速度V0向右运动冲上滑块,已知M=4m,g取10 m/s2,若小球刚好没跃出圆弧的上端,求: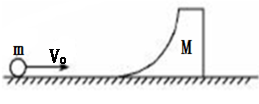
①小球的初速度V0是多少?
②滑块获得的最大速度是多少?