如图所示，静止于A处的离子，经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器，从P点垂直CN进入矩形区域的有界匀强电场，电场方向水平向左。静电分析器通道内有均匀辐向分布的电场，已知圆弧所在处场强为E0，方向沿圆弧半径指向圆心O。离子质量为m、电荷量为q，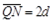
、
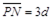，离子重力不计。
（1）求圆弧虚线对应的半径R的大小；
（2）若离子恰好能打在QN板的中点上，求矩形区域QNCD内匀强电场场强E的值；
（3）若撤去矩形区域QNCD内的匀强电场，换为垂直纸面向里的匀强磁场，且离子恰能从QN板下端飞出QNCD区域，求磁场磁感应强度B。
在一次低空跳伞演练中，当直升飞机悬停在离地面224m高处时，伞兵离开飞机做自由落体运动。运动一段时间后，打开降落伞，展伞后伞兵以12.5m/s2的加速度匀减速下降。为了伞兵的安全，要求伞兵落地速度大小最大不得超过5m/s，取g=10m/s2，求：
（1）伞兵展伞时，离地面的高度至少为多少？
（2）着地时相当于从多高处自由落下？
（3）若伞兵的落地速度为5m/s，伞兵在空中的总时间为多少？
汽车自O点出发，从静止开始在平直公路上做匀加速直线运动，途中在6s内先后经过P、Q两根电杆，已知P、Q电杆相距60m，车经过电杆Q时的速率是15m/s，则：
（1）经过P杆时的速率是多少？
（2）车的加速度的大小是多少？
（3）O、Q间的距离是多少？
一物体从某一高度自由下落，经过一高度为2m的窗户用时间0.4s，g取10m/s2。求物体开始下落时的位置距窗户上檐的高度是多少？
汽车在平直的高速公路上行驶的速度为108km/h，若驾驶员发现前方100m处发生了交通事故，马上紧急刹车，刹车后的加速度大小为5m/s2。
（1）汽车刹车后8s的速度和位移各是多少？
（2）该汽车是否会有安全问题？
人站在h高处的平台上，以水平速度v0抛出一个质量为m的小球，以地面为重力势能的零点，不计空气阻力。求：
（1）小球抛出时的机械能是多少？
（2）小球落地时的速度大小v =？