如图所示，左侧装置内存在着匀强磁场和方向竖直向下的匀强电场，装置上下两极板间电势差为U，间距为L，右侧为“梯形”匀强磁场区域ACDH，其中，AH//CD， 
。一束电荷量大小为q、质量不等的带电粒子（不计重力、可视为质点），从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出，接着粒子垂直于AH、由AH的中点M射入“梯形”区域，最后全部从边界AC射出。若两个区域的磁场方向均水平（垂直于纸面向里）、磁感应强度大小均为B，“梯形”宽度
，忽略电场、磁场的边缘效应及粒子间的相互作用。
（1）判定这束粒子所带电荷的种类，并求出粒子速度的大小;
（2）求出这束粒子可能的质量最小值和最大值;
（3）求出（2）问中偏转角度最大的粒子在“梯形”区域中运动的时间。
如图所示，在直角坐标系xoy的第一象限中分布着沿y轴负方向的匀强电场，在第四象限中分布着方向向里垂直纸面的匀强磁场。一个质量为m、电荷量大小为q的带正电微粒，在A点（0，3）以初速度υ0=120m/s平行x轴射入电场区域，然后从电场区域进入磁场，又从磁场进入电场，并且先后只通过x轴上的P点（6，0）和Q点（8，0）各一次。已知该微粒的比荷为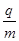
＝102C/kg，微粒重力不计。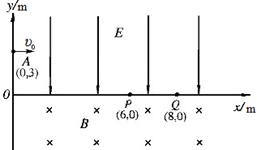
求：
（1）微粒从A到P所经历的时间和加速度的大小；
（2）求出微粒到达P点时速度方向与x轴正方向的夹角；
（3）电场强度E和磁感强度B的大小。
如图甲所示，一对平行光滑导轨固定在水平面上，两导轨间距l＝0.20 m，电阻R＝1.0 Ω。有一导体杆静止地放在导轨上，与两导轨垂直，杆及导轨的电阻皆可忽略不计，整个装置处于磁感应强度B＝0.50 T的匀强磁场中，磁场方向竖直向下．现用一外力F沿导轨方向拉杆，使之做匀加速运动，测得力F与时间t的关系如图乙所示．求出杆的质量m和加速度a大小。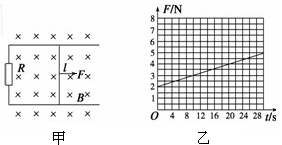
如图所示，一带电小球质量m=1kg，用长度L=1m绝缘细线悬挂在水平向右的匀强电场中，静止时悬线与竖直方向成θ= 53°，已知sin53°=0.8，cos53°=0.6，取重力加速度g=10m/s2。
(1)求小球所受的电场力的大小F；
(2)若仅将电场强度大小突然减小为原来的
，求小球摆到最低点时的速度大小υ和细线对小球的拉力大小T。
（8分) 如图所示，水平放置的两根平行金属导轨相距L= 0.2m，上面静置一质量m= 0.04kg的均匀金属棒ab，且与导轨垂直，导轨和棒ab电阻忽略不计，电源电动势E= 6V、内阻r= 0.5Ω。滑动变阻器调到R= 2.5Ω时，要使棒ab对导轨的压力恰好为零，需在棒ab所在位置施加一个与棒ab垂直的水平匀强磁场，问：(取重力加速度g=10m/s2)
（1）流过棒ab的电流多大？
（2）该匀强磁场的方向如何？
（3）该匀强磁场的磁感应强度为多大？
如图，天花板下悬挂着用两根长为L＝1. 0m的细线连接a、b两个小球。a球质量ma =0.7kg，b球质量为mh＝0. 9kg。现在b球上施加一从零开始缓慢增大的水平力F，当F＝122N时，这个力不再变化。求力F作用的服中系统增加的机械能。