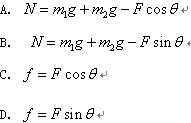如图所示,长为a、宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.O点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m、电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为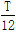 ,最后恰不能从上边界射出的粒子在磁场中经历的时间为
,最后恰不能从上边界射出的粒子在磁场中经历的时间为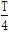 ,不计重力和粒子之间的相互作用,则( )
,不计重力和粒子之间的相互作用,则( )
A.粒子速度大小为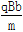 |
| B.粒子做圆周运动的半径为3b |
C.a的长度为(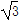 +1)b +1)b |
| D.最后从磁场上边界飞出的粒子一定从上边界的中点飞出 |
静止置于水平地面的一物体质量为m=57 kg,与水平地面间的动摩擦因数为0.43,在F=287 N的水平拉力作用下做匀变速直线运动,则由此可知物体在运动过程中第5个7秒内的位移与第11个3秒内的位移比为( )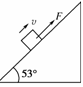
| A.2∶1 | B.1∶2 | C.7∶3 | D.3∶7 |
一个质点做方向不变的直线运动,加速度的方向始终与速度方向相同,但加速度大小逐渐减小直至为零,在此过程中( )
| A.速度逐渐减小,当加速度减小到零时,速度达到最小值 |
| B.速度逐渐增大,当加速度减小到零时,速度达到最大值 |
| C.位移逐渐增大,当加速度减小到零时,位移将不再增大 |
| D.位移逐渐减小,当加速度减小到零时,位移达到最小值 |
伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次。假设某次试验伽利略是这样做的:在斜面上任取三个位置A、B、C,让小球分别由A、B、C滚下,如图所示。设A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3, 小球由A、B、C运动到斜面底端时的速度分别为v1、v2、v3,则下列关系式中正确,并且是伽利略用来证明小球沿光滑斜面向下的运动是匀变速直线运动的是( )
A.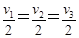 B.
B.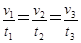 C.
C.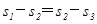 D.
D.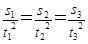
“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下的一种极限运动。某人做蹦极运动,所受绳子拉力F的大小随时间t变化的情况如图所示。将蹦极过程近似为在竖直方向的运动,重力加速度为g。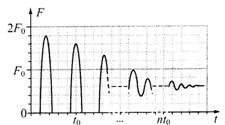
据图可知,此人在蹦极过程中最大加速度约为
| A.g | B.2g | C.3g | D.4g |
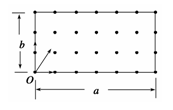
如图所示,质量分别为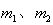 的两个物体通过轻弹簧连接,在力
的两个物体通过轻弹簧连接,在力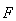 的作用下一起沿水平方向做匀速直线运动(
的作用下一起沿水平方向做匀速直线运动(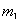 在地面,
在地面,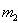 在空中),力
在空中),力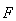 与水平方向成
与水平方向成
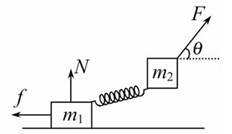
则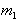 所受支持力N和摩擦力
所受支持力N和摩擦力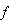 正确的是
正确的是