从含有两件正品a1,a2和一件次品b1的3件产品中每次任取1件,
每次取出后不放回,连续取两次.
(1)求取出的两件产品中恰有一件次品的概率;
(2)如果将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的两件产品中恰有一件次品的概率是多少?
已知函数
(其中常数
),
是奇函数.
(Ⅰ)求
的表达式;
(Ⅱ)讨论
的单调性,并求
在区间[1,2]上的最大值和最小值.
设
的内角
的对边长分别为
,且
.
(Ⅰ) 求
的值;
(Ⅱ)求
的值.
在甲、乙等6个单位参加的一次"唱读讲传"演出活动中,每个单位的节目集中安排在一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
已知
是首项为19,公差为-2的等差数列,
为
的前
项和.
(Ⅰ)求通项
及
;
(Ⅱ)设
是首项为1,公比为3的等比数列,求数列
的通项公式及其前
项和
.
在数列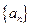 中,
中,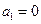 ,且对任意
,且对任意 .
.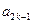 ,
,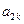 ,
, 成等差数列,其公差为
成等差数列,其公差为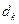 。
。
(Ⅰ)若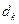 =
= ,证明
,证明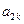 ,
, ,
,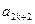 成等比数列(
成等比数列( )
)
(Ⅱ)若对任意 ,
,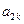 ,
, ,
,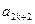 成等比数列,其公比为
成等比数列,其公比为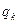 。
。