已知二次函数y=2（x﹣3）2+1，下列说法：
①其图象的开口向下；
②其图象的对称轴为直线x=﹣3；
③其图象顶点坐标为（3，﹣1）；
④当x＜3时，y随x的增大而减小．
则其中说法正确的有
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，已知直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2AD，点E、F分别是AB、BC边的中点，连接AF、CE交于点M，连接BM并延长交CD于点N，连接DE交AF于点P，则结论：①∠ABN=∠CBN； ②DE∥BN； ③△CDE是等腰三角形； ④
； ⑤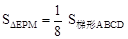
，正确的个数有【】
A. 5个 B. 4个 C. 3个 D. 2个
某校团委与社区联合举办“保护地球，人人有责”活动，选派20名学生分三组到120个店铺发传单，若第一、二、三小组每人分别负责8、6、5个店铺，且每组至少有两人，则学生分组方案有【】
| A． 6种 | B． 5种 | C． 4种 | D．3种 |
如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D， 点E为AC的中点，连接DE，则△CDE的周长为【】
| A． 20 | B． 12 | C． 14 | D． 13 |
若（a－1）2+|b－2|=0，则（a－b）2012的值是【】
| A．－1 | B． 1 | C． 0 | D．2012 |
如图所示，四边形ABCD是边长为4cm的正方形，动点P在正方形ABCD的边上沿着A→B→C→D的路径以1cm/s的速度运动，在这个运动过程中△APD的面积s(cm2)随时间t（s）的变化关系用图象表示，正确的是【】