以原点为圆心,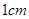
为半径的圆分别交
、
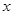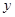轴的正半轴于A、B两点,点P的坐标为
．
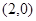（1）如图一，动点Q从点B处出发，沿圆周按顺时针方向匀速运动一周,设经过的时间为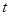
秒，当
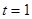时，直线PQ恰好与⊙O第一次相切，连接OQ．求此时点Q的运动速度（结果保留
）；
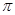（2）若点Q按照⑴中的方向和速度继续运动，
①当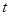为何值时，以O、P、Q为顶点的三角形是直角三角形；
②在①的条件下，如果直线PQ与⊙O相交，请求出直线PQ被⊙O所截的弦长．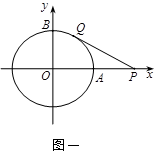
计算：（1）︱-5︱+
+2-1-sin30°；（2）(x-y+
)( x+y-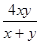
)．
（1）计算：
；（2）化简：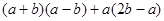
.
已知x是一元二次方程x2－2x＋1＝0的根，求代数式
的值．
如图，已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F，∠ADC的平分线DG交边AB于G。
（1）求证：AF=GB；
（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形，并说明理由．
已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，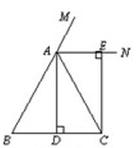
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明.