如图,在四边形ABCD中,AB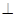 BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.
BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.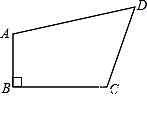
已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),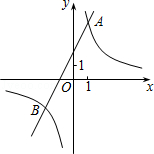
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)若P为Y轴上得一点,连接PA、PB,△PAB的面积为6,求P点的坐标。
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.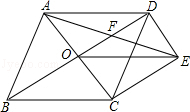
(1)求证:OE=CD
(2)若菱形ABCD的边长为4, ∠ABC=60°,求AE的长.
如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.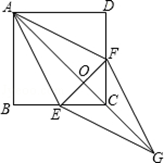
(1)求证:BE=DF,0E=0F
(2)求证:四边形AEGF是菱形.
如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
求证:四边形DBEF是矩形;