小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（B，F，D在同一条直线上）．一直小敏的眼睛与地面距离为1．5m，求这栋建筑物CD的高度（参考数据：
，结果保留整数）
佳佳果品店刚试营业，就在批发市场购买某种水果销售，第一次用1200元购进若干千克水果，并以每千克定价7元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了20％，用1500元所购买的数量比第一次多10千克．
（1）求第一次该种水果的进价是每千克多少元?
（2）佳佳果品店在第二次进货后，以每千克定价7元售出200千克水果后，因出现高温天气，水果不易保鲜，为减少损失，便以定价的4折售完剩余的水果，该果品店在这两次销售中，总体上是盈利还是亏损（不考虑其它因素）?若赔钱，赔多少?若赚钱，赚多少?
如图，在平面直角坐标系中，反比例函数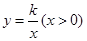
的图象和矩形ABCD在第一象限，AD平行于
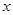轴，且AB=2，AD=4，点A的坐标为（2，6）．
（1）直接写出B、C、D三点的坐标．
（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式．
如图，△ABC中，AB=AC，AD、AE分别是∠BAC和∠BAC的外角的平分线，BE⊥AE
（1）求证：DA⊥AE；
（2）试判断AB与DE是否相等?并证明你的结论．
已知正比例函数
和反比例函数的图象交于点A（m，一2）．
（1）求反比例函数的解析式；
（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量
的取值范围；
（3）若双曲线上点c（2，n）沿OA方向平移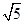
个单位长度得到点B，判断四边形OABC的形状并证明你的结论．
如图，在□ABCD中，AE平分∠BAD交DC于点E，AD=5cm，AB=8cm．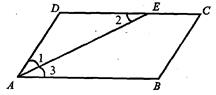
（1）求EC的长；
（2）作∠BCD的平分线交AB于F，求证：四边形AECF为平行四边形