如图,足够长的光滑平行金属导轨MN、PQ固定在一水平面上,两导轨间距L =0.2m,电阻R =0.4Ω,电容C=2 μF,导轨上停放一质量m =0.1kg、电阻r =0.1Ω的金属杆CD,导轨电阻可忽略不计,整个装置处于方向竖直向上B ="0.5T" 的匀强磁场中。现用一垂直金属杆CD的外力F沿水平方向拉杆,使之由静止开始向右运动。求:
(1)若开关S闭合,力F恒为0.5N, 求CD运动的最大速度;
(2)若开关S闭合,使CD以⑴问中的最大速度匀速运动,现使其突然停止并保持静止不动当CD停止下来后,求通过导体棒CD的总电量;若开关S断开,在力F作用下,CD由静止开始作加速度a =5m/s2的匀加速直线运动,请写出电压表的读数U随时间t变化的表达式。
一物体从离地面180m高度处由静止开始自由下落,下落过程中所受阻力不计,已知当地重力加速度大小10m/s2,试求:
(1)经过长时间物体落地;
(2)物体落地时的速度大小;
(3)在落地前的最后1s内下降的高度。
一个质点以初速度v0=2m/s开始做匀变速直线运动,经过t =4s,前进位移x=16m,试求:
(1)质点的加速度大小
(2)第6s末质点的速度大小
(3)质点前6s内的平均速度大小
如图所示的空间分为Ⅰ、Ⅱ、Ⅲ三个区域,各边界面相互平行,Ⅰ区域存在匀强电场,电场强度E=1.0×104V/m,方向垂直边界面向右.Ⅱ、Ⅲ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为B1=2.0T、B2=4.0T.三个区域宽度分别为d1=5.0m、d2= d3=6.25m,一质量m=1.0×10-8kg、电荷量q=1.6×10-6C的粒子从O点由静止释放,粒子的重力忽略不计.试求:
⑴粒子离开Ⅰ区域时的速度大小v;
⑵粒子在Ⅱ区域内运动的时间t;
⑶粒子离开Ⅲ区域时速度与边界面的夹角α.
如图所示,一质量为m,电荷量为q的粒子从容器A下方小孔S1飘入电势差为U的加速电场,然后让粒子从小孔S3垂直进入磁感应强度为B的磁场中,最后打到底片D上, 粒子的重力忽略不计。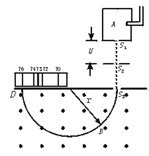
(1)粒子在S1、S2之间做什么运动? 在S2、S3之间做何种运动,在磁场区域将做何种运动?
(2)粒子刚进入磁场时的速度大小
(3)若粒子最终打到底片的D点, S3距离D多远?
如图所示,两平行金属导轨间的距离L=0.40m,金属导轨所在的平面与水平面夹角θ=37º,在导轨所在平面内,分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场。金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源。现把一个质量m=0.04kg的导体棒ab放在金属导轨上,导体棒恰好静止。导体棒与金属导轨垂直、且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5Ω,金属导轨的其它电阻不计,g取10m/s2。已知sin37º=0.60,cos37º=0.80,试求: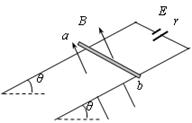
⑴通过导体棒的电流;
⑵导体棒受到的安培力大小;
⑶导体棒受到的摩擦力的大小。