在直角坐标系
中，直线
的参数方程为
为参数），若以O点为极点，
轴正半轴为极轴建立极坐标系，则曲线C的极坐标方程为
。
（1）求曲线C的直角坐标方程及直线的普通方程；
（2）将曲线C上各点的横坐标缩短为原来的
，再将所得曲线向左平移1个单位，得到曲线
，求曲线上的点到直线的距离的最小值
已知圆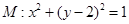
，设点B,C是直线
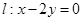上的两点，它们的横坐标分别是
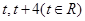，点P在线段BC上，过P点作圆M的切线PA，切点为A
（1）若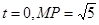
，求直线
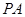的方程；
（2）经过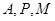
三点的圆的圆心是
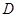，求线段
(
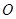为坐标原点）长的最小值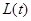
如图，四棱锥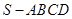
中，
∥
,
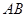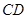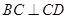，侧面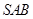
为等边三角形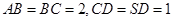
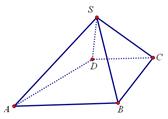
（1）证明：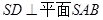
（2）求AB与平面SBC所成角的正弦值
已知：以点C(t,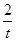
)(t∈R,t≠0)为圆心的圆与
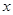轴交于点O,A，与y轴交于点O,B，其中O为原点
（1）求证：△OAB的面积为定值；
（2）设直线y=–2x+4与圆C交于点M,N，若OM=ON，求圆C的方程
已知圆C：
=0
（1）已知不过原点的直线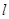
与圆C相切，且在
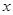轴，
轴上的截距相等，求直线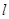的方程；
（2）求经过原点且被圆C截得的线段长为2的直线方程
如图，在正方体
中，
（1）求证：
;
（2）求直线
与直线BD所成的角