已知:以点C(t,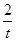 )(t∈R,t≠0)为圆心的圆与
)(t∈R,t≠0)为圆心的圆与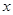 轴交于点O,A,与y轴交于点O,B,其中O为原点
轴交于点O,A,与y轴交于点O,B,其中O为原点
(1)求证:△OAB的面积为定值;
(2)设直线y=–2x+4与圆C交于点M,N,若OM=ON,求圆C的方程
已知函数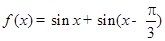 .
.
(Ⅰ)求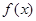 的单调递增区间;
的单调递增区间;
(Ⅱ)在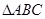 中,角
中,角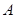 ,
, ,
, 的对边分别为
的对边分别为 .已知
.已知 ,
, ,试判断
,试判断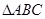 的形状.
的形状.
已知函数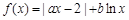 (x>0).
(x>0).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程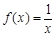 在(0,1]上解的个数.
在(0,1]上解的个数.
已知数列 ,
,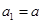 ,且
,且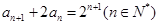 ,
,
(1)若 成等差数列,求实数
成等差数列,求实数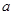 的值;
的值;
(2)数列 能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由。
能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由。
如图,已知椭圆 的上顶点为
的上顶点为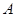 ,离心率为
,离心率为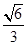 ,若不过点
,若不过点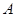 的动直线
的动直线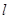 与椭圆
与椭圆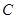 相交于
相交于 、
、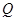 两点,且
两点,且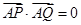 .
.
(Ⅰ)求椭圆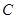 的方程;
的方程;
(Ⅱ)求证:直线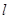 过定点,并求出该定点
过定点,并求出该定点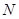 的坐标.
的坐标.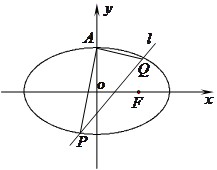
已知定点A(0,1)、B(0,-1)、C(1,0),动点P满足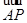 ·
·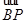 =k|
=k|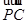 |2.
|2.
(1) 求动点P的轨迹方程,并说明方程表示的曲线.
(2) 当k=2时,求|2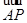 +
+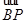 |的最大值和最小值
|的最大值和最小值