已知椭圆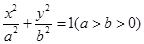 经过点
经过点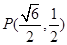 ,离心率为
,离心率为 ,动点M(2,t)(
,动点M(2,t)( ).
).
(1)求椭圆的标准方程;
(2)求以OM为直径且截直线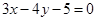 所得的弦长为2的圆的方程;
所得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,证明线段ON的长为定值,并求出这个定值.
已知函数 ,且方程
,且方程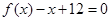 有两个实根
有两个实根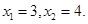
(1)求函数 的解析式;
的解析式;
(2)设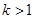 ,解关于
,解关于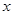 的不等式
的不等式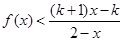 .
.
已知抛物线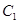 的顶点是双曲线
的顶点是双曲线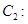
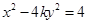 的中心,而焦点是双曲线的左顶点,
的中心,而焦点是双曲线的左顶点,
(1)当 时,求抛物线
时,求抛物线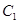 的方程;
的方程;
(2)若双曲线的离心率 ,求双曲线的渐近线方程和准线的方程.
,求双曲线的渐近线方程和准线的方程.
有两颗正四面体的玩具,其四个面上分别标有数字 ,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
(1)求事件“点数之和不小于4”的概率;
(2)求事件“点数之积能被 或
或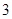 整除”的概率.
整除”的概率.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
(1)写出评委为乙选手打出分数数据的众数,中位数;
(2)求去掉一个最高分和一个最低分后,两位选手所剩数据的平均数和方差,根据结果比较,哪位选手的数据波动小?