某固定在墙上的广告金属支架如图所示，根据要求，
长要超过4米（不含4米），
为的中点，
到
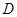的距离比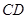
的长小1米，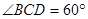
（1）若
，将支架的总长度表示为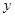
的函数，并写出函数的定义域．（注：支架的总长度为图中线段、
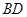和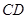的长度之和）
（2）如何设计、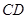的长，可使支架总长度最短．
已知函数
（其中
为自然对数的底）．
（1）求函数
的最小值；
（2）若
，证明：
已知过点
的直线
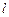与抛物线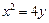
相交于
、
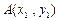两点，
、
分别是该抛物线在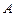
、
两点处的切线，
、
分别是、与直线
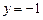的交点．
（1）求直线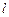的斜率的取值范围；
（2）试比较
与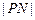
的大小，并说明理由．
已知函数
的图像经过点
和
．
（1）求实数
和
的值；
（2）当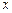
为何值时，
取得最大值．
将一颗质地均匀的正方体骰子（六个面的点数分别为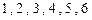
）先后抛掷两次，记第一次出现的点数为
，第二次出现的点数为
．
（1）求事件“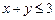
”的概率；（2）求事件“
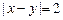”的概率．
在平面直角坐标系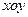
中，已知圆心在直线
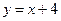上，半径为
的圆C经过坐标原点O，椭圆
与圆C的一个交点到椭圆两焦点的距离之和为10.
（1）求圆C的方程；
（2）若F为椭圆的右焦点，点P在圆C上，且满足
，求点P