将一颗质地均匀的正方体骰子(六个面的点数分别为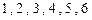 )先后抛掷两次,记第一次出现的点数为
)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(1)求事件“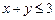 ”的概率;(2)求事件“
”的概率;(2)求事件“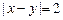 ”的概率.
”的概率.
函数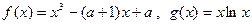
(Ⅰ)若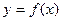 ,
,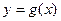 在
在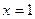 处的切线相互垂直,求这两个切线方程.
处的切线相互垂直,求这两个切线方程.
(Ⅱ)若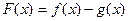 单调递增,求
单调递增,求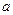 的范围.
的范围.
已知数列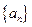 的前
的前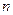 项和为
项和为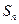 ,对任意的
,对任意的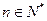 ,点
,点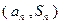 都在直线
都在直线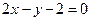 的图像上.
的图像上.
(1)求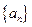 的通项公式;
的通项公式;
(2)是否存在等差数列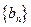 ,使得
,使得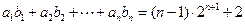 对一切
对一切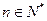 都成立?若存在,求出
都成立?若存在,求出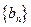 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
已知多面体 中,
中,
 平面
平面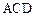 ,
, ∥
∥ ,
,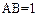 ,
,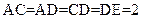 ,
,  、
、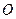 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证: 
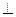 面
面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
设三组实验数据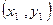 .
.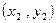 .
.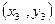 的回归直线方程是:
的回归直线方程是: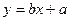 ,使代数式
,使代数式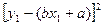
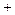
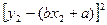
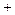
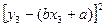 的值最小时,
的值最小时,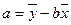 ,
,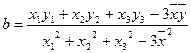 ,(
,(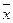 、
、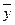 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如下:
| x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
6 |
5 |
6.2 |
8 |
7.1 |
8.6 |
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若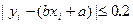 ,即称
,即称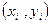 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, , 且
, 且 .\
.\
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在
在 上的最大值.
上的最大值.