函数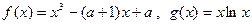
(Ⅰ)若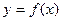 ,
,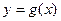 在
在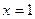 处的切线相互垂直,求这两个切线方程.
处的切线相互垂直,求这两个切线方程.
(Ⅱ)若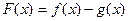 单调递增,求
单调递增,求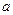 的范围.
的范围.
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.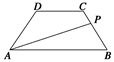
设直线x=1是函数f(x)的图象的一条对称轴,对于任意x∈R,f(x+2)=-f(x),当-1≤x≤1时,f(x)=x3.
(1)证明:f(x)是奇函数;
(2)当x∈[3,7]时,求函数f(x)的解析式.
某工厂生产某种产品,已知该产品的月生产量x(t)与1 t产品的价格p(元/t)之间的关系为:p="24" 200-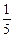 x2,且生产xt的成本为R(元),其中R="50" 000+200x.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
x2,且生产xt的成本为R(元),其中R="50" 000+200x.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两用户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
某工厂生产一种机器的固定成本(即固定投入)为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台,销售的收入函数为R(x)=5x-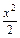 (万元)(0≤x≤5),其中x是产品售出的数量(单位:百台).
(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
(3)年产量是多少时,工厂才不亏本?