设三组实验数据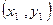 .
.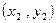 .
.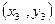 的回归直线方程是:
的回归直线方程是: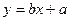 ,使代数式
,使代数式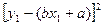
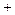
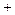
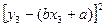 的值最小时,
的值最小时,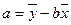 ,
,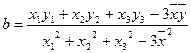 ,(
,(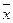 、
、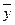 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如下:
| x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
6 |
5 |
6.2 |
8 |
7.1 |
8.6 |
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若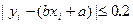 ,即称
,即称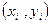 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
椭圆的中心是原点O,它的短轴长为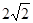 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(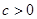 )的准线
)的准线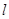 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
(1)求椭圆的方程及离心率;
(2)若 ,求直线PQ的方程;
,求直线PQ的方程;
(3)设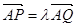 (
(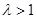 ),过点P且平行于准线
),过点P且平行于准线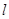 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明 .
.
一条变动的直线L与椭圆 +
+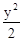 =1交于P、Q两点,M是L上的动点,满足关系|MP|·|MQ|=2.若直线L在变动过程中始终保持其斜率等于1.求动点M的轨迹方程,并说明曲线的形状.
=1交于P、Q两点,M是L上的动点,满足关系|MP|·|MQ|=2.若直线L在变动过程中始终保持其斜率等于1.求动点M的轨迹方程,并说明曲线的形状.
椭圆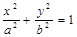
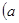 >
> >
>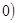 与直线
与直线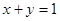 交于
交于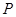 、
、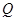 两点,且
两点,且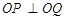 ,其中
,其中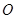 为坐标原点.
为坐标原点.
(1)求 的值;
的值;
(2)若椭圆的离心率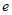 满足
满足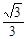 ≤
≤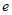 ≤
≤ ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
过椭圆 引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
(1)若 ,求P点坐标;
,求P点坐标;
(2)求直线AB的方程(用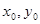 表示);
表示);
(3)求△MON面积的最小值.(O为原点)。
已知A、B为椭圆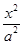 +
+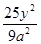 =1上两点,F2为椭圆的右焦点,若|AF2|+|BF2|=
=1上两点,F2为椭圆的右焦点,若|AF2|+|BF2|= a,AB中点到椭圆左准线的距离为
a,AB中点到椭圆左准线的距离为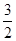 ,求该椭圆方程.
,求该椭圆方程.