(本小题满分12分)在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点.若l与圆x2+y2=1相切,求证:OP⊥OQ;
(本小题满分14分)
如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.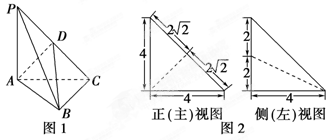
(1) 证明:AD⊥平面PBC;
(2) 在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
在 中,角
中,角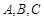 的对边分别为
的对边分别为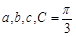 ,
,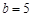 ,
, 的面积为
的面积为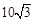 .
.
(1)求 ,
,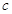 的值;
的值;
(2)求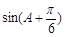 的值.
的值.
已知向量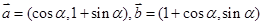
(1) 若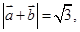 求
求 的值;
的值;
(2) 设 ,求
,求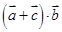 的取值范围.
的取值范围.
已知函数 ,
, ,其中
,其中 .
.
(1)设函数 ,若
,若 在区间
在区间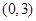 是单调函数,求
是单调函数,求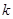 的取值范围;
的取值范围;
(2)设函数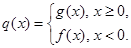 ,是否存在
,是否存在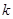 ,对任意给定的非零实数
,对任意给定的非零实数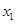 ,存在惟一的非零实数
,存在惟一的非零实数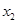 (
(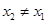 ),使得
),使得 成立?若存在,求
成立?若存在,求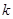 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
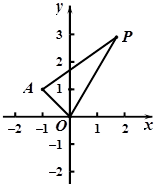
在平面直角坐标系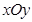 中,已知点
中,已知点
 ,点P是动点,且三角形
,点P是动点,且三角形 的三边所在直线
的三边所在直线
的斜率满足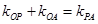 .
.
(1)求点P的轨迹 的方程;
的方程;
(2)设Q是轨迹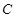 上异于点
上异于点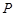 的一个点,若
的一个点,若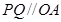 ,直线
,直线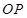 与
与 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得 和
和 的面积满足
的面积满足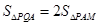 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由.