(本小题满分12分) 定义在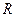
 上的函数
上的函数 同时满足以下条件:①
同时满足以下条件:①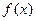 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;②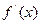 是偶函数;
是偶函数;
③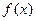 在
在 处的切线与直线
处的切线与直线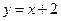 垂直.
垂直.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设 ,若
,若 存在
存在 ,使
,使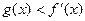 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分) 已知各项均为正数的数列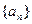 满足:
满足: 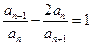 (
( ),且
),且
 .
.
(Ⅰ)求数列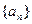 的通项公式;
的通项公式;
( Ⅱ)证明:
Ⅱ)证明: (
( )
)
(Ⅲ)若 ,令
,令 ,设数列
,设数列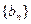 的前
的前 项和为
项和为 (
( ),试比较
),试比较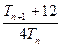 与
与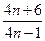 的大小.
的大小.
(本小题满分12分)
四棱锥P—ABCD中,侧面PAD 底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,
底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,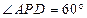 ,E、G分别是BC、PE的中点。
,E、G分别是BC、PE的中点。
(1)求证:AD PE;
PE;
(2)求二面角E—AD—G的正切值。
(本小题满分12分)
如图,圆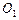 与圆
与圆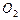 的半径
的半径 都等于1,
都等于1,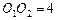 . 过动点
. 过动点 分别作圆
分别作圆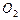 、圆
、圆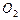 的切线
的切线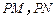 (
(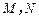 分别为切点),使得|PM|=|PN|.
分别为切点),使得|PM|=|PN|.
试建立适当的坐标系,并求动点 的轨迹方程.
的轨迹方程.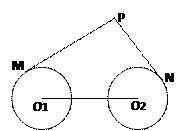
(本小题满分12分)
已知 ,
, ,若·=,
,若·=,
且 ,求
,求 的值
的值