(本小题满分12分)
如图,圆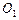 与圆
与圆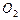 的半径
的半径 都等于1,
都等于1,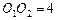 . 过动点
. 过动点 分别作圆
分别作圆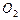 、圆
、圆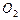 的切线
的切线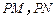 (
(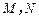 分别为切点),使得|PM|=|PN|.
分别为切点),使得|PM|=|PN|.
试建立适当的坐标系,并求动点 的轨迹方程.
的轨迹方程.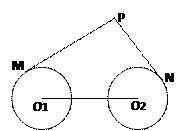
设 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和 且
且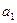 ,
,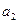 ,
,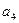 成等比数列.(1)
成等比数列.(1) 证明
证明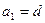 ;(2)求公差
;(2)求公差 的值和数列
的值和数列 的通项公式.
的通项公式.
如图,测量河对岸的塔高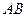 时,可以选与塔
时,可以选与塔 底
底 在同一水平面内的两个测点
在同一水平面内的两个测点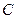 与
与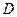 .现测得
.现测得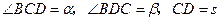 ,并在点
,并在点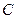 测得塔顶
测得塔顶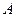 的仰角为
的仰角为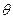 ,求塔高
,求塔高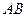 .
.
(本小题共14分)
已知函数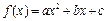 ,其中
,其中 .
.
(Ⅰ)若b>2a,且 的最大值为2,最小值为-4,试求函数f(x)的最小值;
的最大值为2,最小值为-4,试求函数f(x)的最小值;
(Ⅱ)若对任意实数x,不等式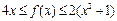 恒成立,且存在
恒成立,且存在 使得
使得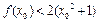 成立,求c的值.
成立,求c的值.
(本小题共13分)
在平面直角坐标系xOy中,经过点(0, 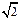 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆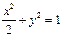 有两个不同的交点P和Q.
有两个不同的交点P和Q.
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量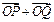 与
与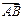 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
(本小题共14分)
已知函数 ,数列
,数列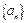 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q
是公比为q
( )的等比数列.若
)的等比数列.若

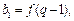

(Ⅰ)求数列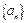 ,
, 的通项公式;
的通项公式;
(Ⅱ)设数列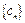 对任意自然数n均有
对任意自然数n均有 ,求
,求 的值.
的值.