(本小题满分12分) 已知各项均为正数的数列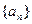 满足:
满足: 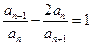 (
( ),且
),且
 .
.
(Ⅰ)求数列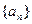 的通项公式;
的通项公式;
( Ⅱ)证明:
Ⅱ)证明: (
( )
)
(Ⅲ)若 ,令
,令 ,设数列
,设数列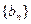 的前
的前 项和为
项和为 (
( ),试比较
),试比较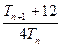 与
与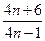 的大小.
的大小.
已知 .
.
(Ⅰ)求 的值
的值
(Ⅱ)求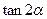 的值
的值
已知函数
(1)求函数 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值;
(2)若 ,求
,求 的值。
的值。
上海某学校要从艺术节活动中所产生的4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加即将在上海举行的世博会的志愿服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
已知 ,若
,若 ,
,
 ,
,
(1)求 ;
;
(2)求 的夹角。
的夹角。
(本小题满分 12分)
12分)
根据下面的要求,求满足 的最小的自然数n。
的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)下图是解决该问题的一个程序,但有2处错误,请找出错误并予以更正。