如图,圆 与
与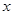 轴相切于点
轴相切于点 ,与
,与 轴正半轴相交于两点
轴正半轴相交于两点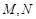 (点
(点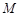 在点
在点 的下方),且
的下方),且 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)过点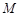 任作一条直线与椭圆
任作一条直线与椭圆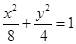 相交于两点
相交于两点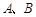 ,连接
,连接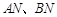 ,求证:
,求证: .
.
如图, 是等边三角形,
是等边三角形,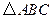 是等腰直角三角形,
是等腰直角三角形,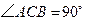 ,
, 交
交 于
于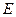 ,
,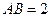 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 .
. 
已知函数 满足
满足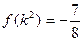 ;
;
(1)求常数k的值;(2)若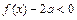 恒成立,求a的取值范围.
恒成立,求a的取值范围.
如图,在四棱锥 中,底面
中,底面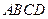 是边长为
是边长为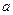 的正方形,侧面
的正方形,侧面
 底面
底面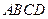 ,
,
若 、
、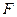 分别为
分别为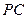 、
、 的中点.
的中点.
(Ⅰ)  //平面
//平面 ;(Ⅱ) 求证:平面
;(Ⅱ) 求证:平面 平面
平面 ;
; 
.已知函数f(x)= 在[0,1]上的最小值为
在[0,1]上的最小值为 ,
,
(1)求f(x)的解析式;(2)证明:f(1)+f(2)+…+f(n)>n- +
+ (n∈N
(n∈N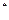 )
)
对于定义域为D的函数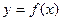 ,若同时满足下列条件:
,若同时满足下列条件:
①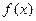 在D内单调递增或单调递减;
在D内单调递增或单调递减;
②存在区间[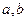 ]
]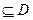 ,使
,使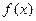 在[
在[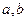 ]上的值域为[
]上的值域为[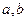 ];那么把
];那么把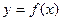 (
(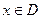 )叫闭函数。
)叫闭函数。
(1)求闭函数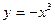 符合条件②的区间[
符合条件②的区间[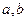 ];
];
(2)判断函数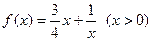 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若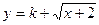 是闭函数,求实数
是闭函数,求实数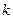 的取值范围。
的取值范围。