对于定义域为D的函数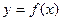 ,若同时满足下列条件:
,若同时满足下列条件:
①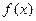 在D内单调递增或单调递减;
在D内单调递增或单调递减;
②存在区间[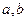 ]
]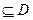 ,使
,使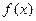 在[
在[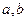 ]上的值域为[
]上的值域为[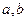 ];那么把
];那么把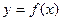 (
(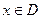 )叫闭函数。
)叫闭函数。
(1)求闭函数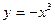 符合条件②的区间[
符合条件②的区间[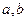 ];
];
(2)判断函数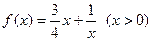 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若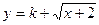 是闭函数,求实数
是闭函数,求实数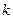 的取值范围。
的取值范围。
已知曲线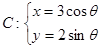 (
(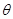 为参数)在同一直角坐标系中,将曲线
为参数)在同一直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线 ,
,
(1)求曲线 的普通方程;
的普通方程;
(2)若点 在曲线
在曲线 上,点
上,点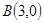 ,当
,当 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点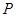 的轨迹方程。
的轨迹方程。
已知抛物线方程为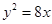 ,
,
(1)直线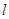 过抛物线的焦点
过抛物线的焦点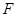 ,且垂直于
,且垂直于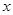 轴,
轴,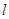 与抛物线交于
与抛物线交于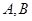 两点,求
两点,求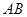 的长度。
的长度。
(2)直线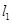 过抛物线的焦点
过抛物线的焦点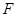 ,且倾斜角为
,且倾斜角为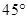 ,直线
,直线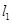 与抛物线相交于
与抛物线相交于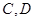 两点,
两点,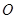 为原点。求△
为原点。求△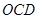 的面积。
的面积。
已知抛物线C的顶点为坐标原点,焦点为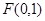 ,
,
(1)求抛物线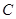 的方程;
的方程;
(2)过点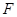 作直线
作直线 交抛物线于
交抛物线于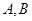 两点,若直线
两点,若直线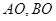 分别与直线
分别与直线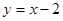 交于
交于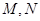 两点,求
两点,求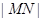 的取值范围.
的取值范围.
已知椭圆 的离心率为
的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
如图,在长方体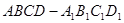 中,
中, ,点E在棱
,点E在棱 上移动.
上移动.
(1)证明: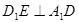 ;
;
(2)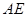 等于何值时,二面角
等于何值时,二面角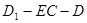 为
为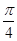 .
.