心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女生被抽到的人数为X, 求X的分布列及数学期望E(X) .
附表及公式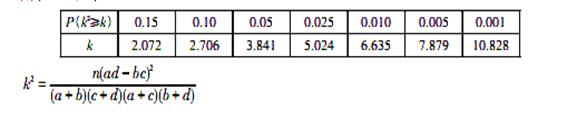
已知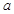 、
、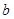 、
、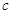 为正实数,
为正实数,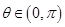 .
.
(1)当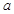 、
、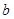 、
、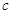 为
为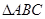 的三边长,且
的三边长,且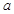 、
、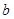 、
、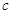 所对的角分别为
所对的角分别为 、
、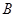 、
、 .若
.若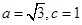 ,且
,且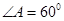 .求
.求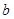 的长;
的长;
(2)若 .试证明长为
.试证明长为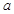 、
、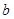 、
、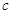 的线段能构成三角形,而且边
的线段能构成三角形,而且边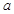 的对角为
的对角为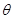 .
.
对于函数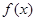 ,若在定义域存在实数
,若在定义域存在实数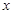 ,满足
,满足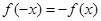 ,则称
,则称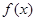 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数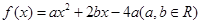 ,试判断
,试判断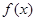 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设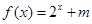 是定义在
是定义在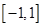 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为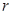 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?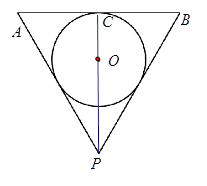
设等差数列 的公差为
的公差为 ,且
,且 .若设
.若设 是从
是从 开始的前
开始的前 项数列的和,即
项数列的和,即 ,
, ,如此下去,其中数列
,如此下去,其中数列 是从第
是从第 开始到第
开始到第 )项为止的数列的和,即
)项为止的数列的和,即 .
.
(1)若数列 ,试找出一组满足条件的
,试找出一组满足条件的 ,使得:
,使得:  ;
;
(2)试证明对于数列 ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列 中的各数都为平方数;
中的各数都为平方数;
(3)若等差数列 中
中 .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列 ,使得
,使得 为等比数列,如存在,就求出数列
为等比数列,如存在,就求出数列 ;如不存在,则说明理由.
;如不存在,则说明理由.
已知抛物线 .
.
(1)若圆心在抛物线 上的动圆,大小随位置而变化,但总是与直线
上的动圆,大小随位置而变化,但总是与直线 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;
(2)抛物线 的焦点为
的焦点为 ,若过
,若过 点的直线与抛物线相交于
点的直线与抛物线相交于 两点,若
两点,若 ,求直线
,求直线 的斜率;
的斜率;
(3)若过 正半轴上
正半轴上 点的直线与该抛物线交于
点的直线与该抛物线交于 两点,
两点, 为抛物线上异于
为抛物线上异于 的任意一点,记
的任意一点,记 连线的斜率为
连线的斜率为 试求满足
试求满足 成等差数列的充要条件.
成等差数列的充要条件.