某地区为了了解某地区高中生的身体发育情况，对某一中学的随机抽取的50名学生的体重进行了测量，结果如下：（单位：kg）
42,38,29,36,41,43,54,43,34,44,40,59,39,42,44,50,37,44,45,29,48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,,67,53，49,65,47,54,63,58,43,46,58.
| 分组 |
频数 |
频率 |
频率/组距 |
| [27,32) |
|
0.06 |
|
| [32,37) |
|
0.06 |
|
| [37,42) |
9 |
|
|
| [42,47) |
|
|
0.064 |
| [47,52) |
7 |
|
|
| [52,57) |
5 |
|
|
| [57,62) |
4 |
|
|
| [62,67) |
|
0.06 |
|
（1）若以组距为5，完成下面样本频率分布表：
（2）根据（1）中的频率分布表，画出频率分布直方图；
（3）若本地区学生总人数为3000人，试根据抽样比例，估计本地区学生体重在区间[37,57]内所占的人数约为多少人？
已知△ABC中的内角A,B,C对边分别为a,b,c，
sin2C+2cos2C+1=3，c=.
（1）若cosA＝
，求a；
（2）若2sinA=sinB，求△ABC的面积．
已知圆x2＋y2－6mx－2(m－1)y＋10m2－2m－24＝0(m∈R)．
(1)求证：不论m取什么值，圆心在同一直线l上；
(2)与l平行的直线中，哪些与圆相交，相切，相离．
已知圆C：(x－1)2＋(y－2)2＝25，直线l：(2m＋1)x＋(m＋1)y－7m－4＝0(m∈R)．
(1)求证：不论m取什么实数，直线l与圆C恒交于两点；
(2)求直线被圆C截得的弦长最小时直线l的方程．
已知以点C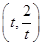
(t∈R，t≠0)为圆心的圆与x轴交于点O、A，与y轴交于点O、B，其中O为原点．
(1)求证：△AOB的面积为定值；
(2)设直线2x＋y－4＝0与圆C交于点M、N，若|OM|＝|ON|，求圆C的方程；
(3)在(2)的条件下，设P、Q分别是直线l：x＋y＋2＝0和圆C的动点，求|PB|＋|PQ|的最小值及此时点P的坐标．
已知圆C过点P(1，1)，且与圆M：(x＋2)2＋(y＋2)2＝r2(r＞0)关于直线x＋y＋2＝0对称．
(1)求圆C的方程；
(2)过点P作两条相异直线分别与圆C相交于A、B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．