已知函数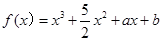 (
( 为常数),其图象是曲线
为常数),其图象是曲线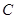 .
.
(1)当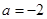 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为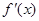 ,若存在唯一的实数
,若存在唯一的实数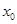 ,使得
,使得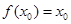 与
与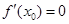 同时成立,求实数
同时成立,求实数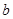 的取值范围;
的取值范围;
(3)已知点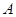 为曲线
为曲线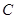 上的动点,在点
上的动点,在点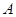 处作曲线
处作曲线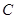 的切线
的切线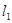 与曲线
与曲线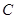 交于另一点
交于另一点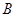 ,在点
,在点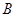 处作曲线
处作曲线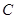 的切线
的切线 ,设切线
,设切线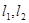 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数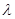 ,使得
,使得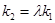 ?若存在,求出
?若存在,求出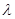 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在直线三棱柱ABC—A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.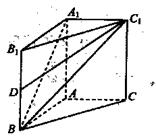
(Ⅰ)求证:AC⊥A1B;
(Ⅱ)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
设数列{an}是等差数列,数列{bn}的前n项和Sn满足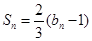 且
且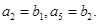
(Ⅰ)求数列{an}和{bn}的通项公式:
(Ⅱ)设Tn为数列{Sn}的前n项和,求Tn.
已知数列 的前
的前 项和
项和 (
( 为正整数)。
为正整数)。
(1) 令 ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2) 令 ,
, ,求使得
,求使得 成立的最小正整数
成立的最小正整数 ,并证明你的结论.
,并证明你的结论.
在△ 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,且
,且
(1)求角B的大小;
(2)若 且
且 ,求
,求 的取值范围.
的取值范围.
已知等差数列 满足:
满足:
(1) 求数列 的前20项的和;
的前20项的和;
(2) 若数列 满足:
满足: ,求数列
,求数列 的前
的前 项和.
项和.