某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
| |
用煤(吨) |
用电(千瓦) |
产值(万元) |
| 甲产品 |
7 |
20 |
8 |
| 乙产品 |
3 |
50 |
12 |
但国家每天分配给该厂的煤、电有限,每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产量最大?最大日产量为多少?
(本小题满分12分)
设直线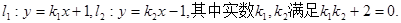
(I)证明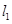 与
与 相交;
相交;
(II)证明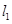 与
与 的交点在椭圆
的交点在椭圆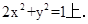
(本小题满分12分)
编号为 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
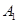 |
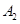 |
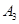 |
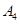 |
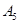 |
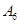 |
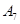 |
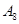 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
 |
 |
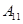 |
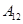 |
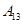 |
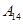 |
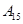 |
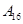 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |
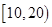 |
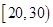 |
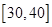 |
| 人数 |
(Ⅱ)从得分在区间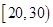 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
(本小题满分12分)
如图,四棱锥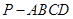 中,底面ABCD为平行四边形,
中,底面ABCD为平行四边形,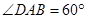 ,
,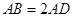 ,
,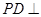 底面ABCD.
底面ABCD.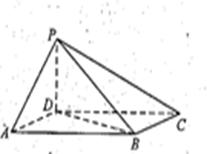
(I)证明: ;
;
(II)设PD=AD=1,求棱锥D-PBC的高.
(本小题满分12分)
已知等比数列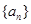 中,
中,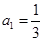 ,公比
,公比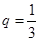 .
.
(I)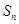 为
为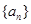 的前n项和,证明:
的前n项和,证明:
(II)设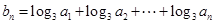 ,求数列
,求数列 的通项公式.
的通项公式.
(满分14分)设函数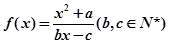 .若方程
.若方程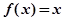 的根为0和2,且
的根为0和2,且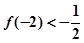 .
.
(1). 求函数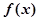 的解析式;
的解析式;
(2) 已知各项均不为零的数列 满足:
满足: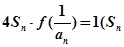 为该数列的前n项和),求该数列的通项
为该数列的前n项和),求该数列的通项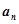 ;
;
(3)如果数列 满足
满足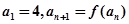 .求证:当
.求证:当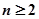 时,恒有
时,恒有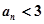 成立.
成立.