某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计.结果如图: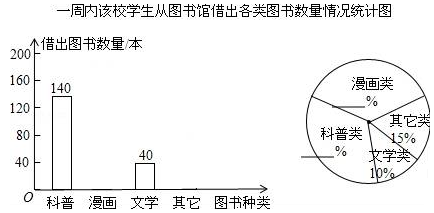
请你根据统计图中的信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)该校学生最喜欢借阅哪类图书?
(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应的确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2 100元,每件衬衫应降价多少元?
阅读下面的例题:
解方程
解:当x≥0时,原方程化为x2-x-2=0,解得:x1=2,x2=-1(不合题意,舍去);
当x<0时,原方程化为x2+ x-2=0,解得:x1=1,(不合题意,舍去)x2=-2;
∴原方程的根是x1=2,x2=-2.
请参照例题解方程 .
.
如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.
已知一元二次方程kx2+(2k-1)x+k+2=0有两个不相等的实数根,求k的取值范围.
解下列方程:
(1)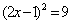
(2)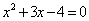
(3)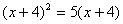
(4)x2+4x=2