如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=18cm.
(1)求线段CB的长;
(2)求线段MN的长.
解方程:
化简:
如图,正方形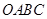 的面积为9,点
的面积为9,点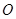 为坐标原点,点
为坐标原点,点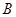 在函数
在函数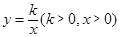 的图象上,点
的图象上,点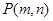 是函数
是函数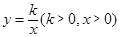 的图象上任意一点,边点
的图象上任意一点,边点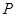 分别作
分别作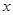 轴、
轴、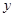 轴的垂线,垂足分别为
轴的垂线,垂足分别为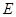 、
、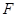 ,并设矩形
,并设矩形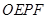 和正方形
和正方形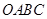 不重合部分的面积为S.
不重合部分的面积为S.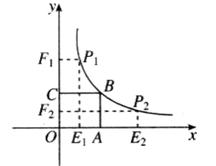
⑴求
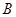 点的坐标和
点的坐标和 的值;
的值;⑵当
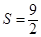 时,求
时,求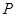 点的坐标;
点的坐标;⑶写出
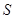 关于
关于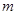 的函数关系式.
的函数关系式.
如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.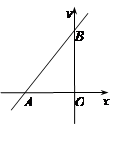
(1)求k的值;
(2)若P为直线AB上一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形,求点P的坐标;
(3)在(2)的条件下,连结PO,△PBO是等腰三角形吗?如果是,试说明理由,如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为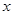 (时),两车之间的距离为
(时),两车之间的距离为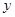 (千米),图中的折线表示从两车出发至快车到达乙地过程中
(千米),图中的折线表示从两车出发至快车到达乙地过程中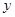 与
与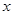 之间的函数关系.
之间的函数关系.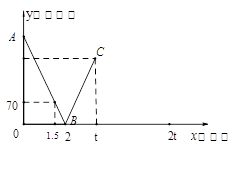
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中
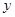 关于
关于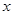 的函数的大致图象.
的函数的大致图象.