如下图所示,在空间有一直角坐标系xOy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是它们的理想边界,OP上方区域Ⅰ中磁场的磁感应强度为B。一质量为m、电荷量为q的质子(不计重力,不计质子对磁场的影响)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直打在x轴上的Q点(图中未画出)。试求:
(1)区域Ⅱ中磁场的磁感应强度大小;
(2)Q点到O点的距离。
如图所示,电源电动势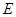 =10V,
=10V,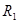 =3Ω,
=3Ω,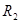 =6Ω,
=6Ω,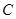 =30μF,闭合开关
=30μF,闭合开关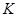 ,电路稳定后, 路端电压
,电路稳定后, 路端电压 =9V,
=9V,
求:(1)电路稳定后通过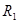 的电流;(2)电源的内阻
的电流;(2)电源的内阻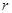 ;
;
(3)若开关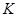 断开,求这以后通过
断开,求这以后通过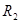 的总电量。
的总电量。
如图所示,在光滑水平面AB上,水平恒力F推动质量为m="1" kg的物体从A点由静止开始做匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变,最高能到达C点,用速度传感器测量物体的瞬时速度,表中记录了部分测量数据),求:
| t(s) |
0.0 |
0.2 |
0.4 |
… |
2.2 |
2.4 |
2.6 |
… |
| v(m/s) |
0.0 |
0.4 |
0.8 |
… |
3.0 |
2.0 |
1.0 |
… |
(1)恒力F的大小.
(2)斜面的倾角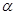 .
.
(3)t="2.1" s时物体的速度.
一物体在地球表面重90N,它在以a=g/3的加速度(g为地球表面上重力加速度)加速上升的火箭中的视重为40N,则此火箭离地球表面的距离为地球半径的多少倍?
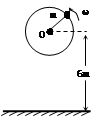
一个人用一根长L=1m,只能承受T=46N拉力的绳子,拴着一个质量为m=1kg的小球,在竖直面内做圆周运动,已知转轴O离地的距离H=6m,如图所示,此人必须用多大的角速度转动小球方能使小球到达最低点时绳子被拉断,绳子拉断后,小球的水平射程是多大?
如图所示,一质量为m=1kg的滑块沿着粗糙的圆弧轨道滑行,当经过最高点时速度V=2m/s,已知圆弧半经R=2m,滑块与轨道间的摩擦系数μ=0.5,则滑块经过最高点时的摩擦力大小为多少?