观察下表三行数的规律,回答下列问题:
| |
第1列 |
第2列 |
第3列 |
第4列 |
第5列 |
第6列 |
… |
| 第1行 |
-2 |
4 |
-8 |
a |
-32 |
64 |
… |
| 第2行 |
0 |
6 |
-6 |
18 |
-30 |
66 |
… |
| 第3行 |
-1 |
2 |
-4 |
8 |
-16 |
b |
… |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
如图,已知△ABC是等边三角形,BD是△ABC的中线,延长BC至E,使CE=CD,连接DE,试说明BD=ED的理由.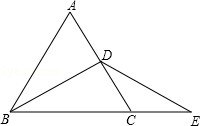
如图,BD是等边△ABC的高,E是BC延长线上一点,且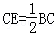 .
.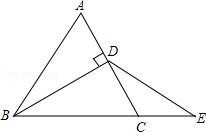
(1)直接写出CE与CD的数量关系;
(2)试说明△BDE是等腰三角形.
如图,在△ABC中,∠B=∠C=30°,D是BC的中点,连接AD,求∠BAD与∠ADC的度数.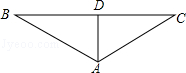
如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F.
(1)作出∠CAB的平分线AE;
(2)试说明△CEF是什么三角形?并证明你的结论.
如图,△ABC中,AD平分∠BAC,CD∥AB交AD于D.试判断△ADC的形状,并说明你的理由.