如图,抛物线y=ax2+bx+c的顶点为C(0,﹣ ),与x轴交于点A、B,连接AC、BC,得等边△ABC.T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒
),与x轴交于点A、B,连接AC、BC,得等边△ABC.T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒 个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动.设运动时间为t秒.
个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动.设运动时间为t秒.
(1)求二次函数的解析式;
(2)设△TSC的面积为S,求S关于t的函数解析式;
(3)以点T为圆心,TB为半径的圆与射线BC交于点E,试说明:在点T运动的过程中,线段ED的长是一定值,并求出该定值.
如图,在△ABC中,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连接BF.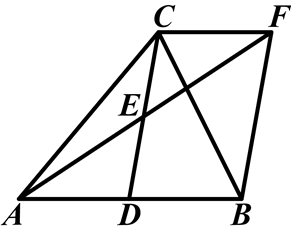
(1)求证:DB=CF;
(2)如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
如图,已知在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于点G.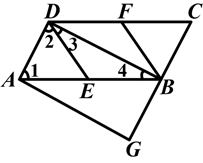
(1)求证:△ADE≌△CBF;
(2)若DE=BE,则四边形AGBD是什么特殊四边形?并证明你的结论.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积.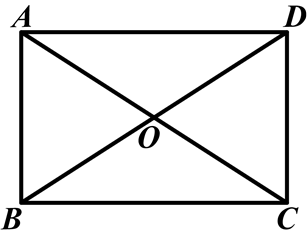
如图,在直角梯形ABCD中,AD∥BC,AD⊥DC,点A关于对角线BD的对称点F刚好落在腰DC上,连接AF交BD于点E,AF的延长线与BC的延长线交于点G,M,N分别是BG,DF的中点.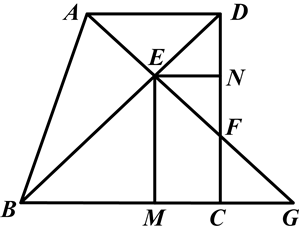
(1)求证:四边形EMCN是矩形;
(2)若AD=2,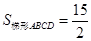 ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.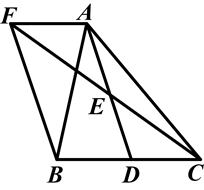
(1)BD与CD有什么数量关系?并说明理由.
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.