如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
回答下列问题:
(1)求证:△GAF∽△GBA;
(2)求证:AF2=FG•FC;
(3)设y=AF2+AG2,FG=x,求y与x的函数关系式;(不要求写出自变量的取值范围)
(4)探究BF2、FG2、GC2之间的关系,证明你的结论.
先化简再求代数式的值:
5a2+[a 2+(5a2-2a)-2(a 2-3a)],其中 ;
;
解方程组: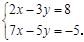
先观察图形,阅读相关文字后,再回答问题.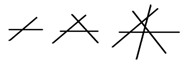
两条直线相交,最多有1个交点;
三条直线相交,最多有3个交点;
四条直线相交,最多有6个交点;
…… ……
问题:10条直线相交,最多有几个交点?
小张、小王、小李同时从湖边同一地点出发,绕湖行走.小张的速度是5.4千米/小时,小王的速度是4.2千米/小时,他们两人同向行走,小李与他们反向行走,半小时后小李和小张相遇,再经过5分钟,小李与小王相遇.那么绕湖一周的行程是多少千米?
甲、乙两品牌服装的单价分别为a元和b元,现实行打折销售,甲种服装按8折(即原价的80%)销售,乙种服装按7折销售,若购买两种品牌服装各一件,共需多少元?