如图,直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4>kx+b的解集.
已知∠AOB=60°,半径为3cm的⊙P沿边OA从右向左平行移动,与边OA相切的切点记为点C.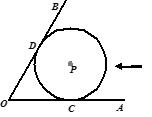
(1)⊙P移动到与边OB相切时(如图),切点为D,求劣弧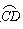 的长;
的长;
(2)⊙P移动到与边OB相交于点E,F,若EF=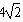 cm,求OC的长;
cm,求OC的长;
如图,抛物线y= x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
(1)求a的值;
(2)求A,B的坐标;
(3)以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.
如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75)
一枚棋子放在边长为1个单位长度的正六边形
ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在
一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀
后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1
个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位
长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法
求解)
为了解某校“振兴阅读工程”的开展情况,教育部门对该校初中生的

阅读情况进行了随机问卷调查,绘制了如下图表:
初中生喜爱的文学作品种类调查统计表
| 种类 |
小说 |
散文 |
传记 |
科普 |
军事 |
诗歌 |
其他 |
| 人数 |
72 |
8 |
21 |
19 |
15 |
2 |
13 |
根据上述图表提供的信息,解答下列问题:
(1)喜爱小说的人数占被调查人数的百分比是多少?初中生每天阅读时间的中位数在哪
个时间段内?
(2)将写读后感、笔记积累、画圈点读等三种方式称为有记忆阅读.请估计该校现有的
2000名初中生中,能进行有记忆阅读的人数约是多少?