今年3月5日,我校组织全体学生参加了“走出校门,服务社会”的活动.九年级三班同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图.请根据同学所作的两个图形.解答:
(1)九年级三班有多少名学生;
(2)补全直方图的空缺部分;
(3)若九年级有800名学生,估计该年级去敬老院的人数.
在如图所示的2004年1月份日历中,
| 星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
| 1 |
2 |
3 |
||||
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
29 |
30 |
31 |
用一个长方形的方框圈出任意3×3个数.如果从左下角到右上角的“对角线”上的3个数字的和为45,那么这9个数的和为,在这9个日期中,最后一天是号;
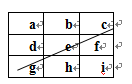
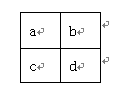
用一个长方形方框圈出任意2×2个数(如4,5,11,12),你能发现这四个数有怎样的关系?请用一个等式表示a,b,c,d 之间的关系.
某一中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问: 聪聪家与刚刚家相距多远?
如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).
聪聪家向西210米所表示的数是多少?
你认为可用什么办法求数轴上两点之间的距离?
若(a+2)2+|b-a|=0,求代数式a3-3a2b+3ab2-b3的值。
当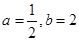 时,求
时,求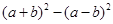 的值。
的值。
如图,已知直线y =-x+4与反比例函数 的图象相交于点A(-2,a),并且与x轴相交于点B.
的图象相交于点A(-2,a),并且与x轴相交于点B.求a的值.
求反比例函数的表达式.
求△AOB的面积.
