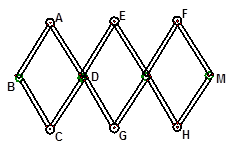
如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.

(1)当点P运动到线段OA的中点时,点C的坐标为 ;
(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;
(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.
如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.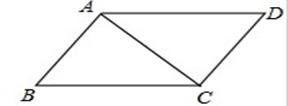
(1)求证:四边形ABCD是平行四边形;
(2)若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?
如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.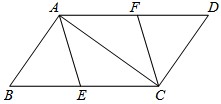
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形。求证:四边形ABCD是矩形.
一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
| A |
B |
C |
D |
E |
平均分 |
标准差 |
|
| 数学 |
71 |
72 |
69 |
68 |
70 |
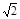 |
|
| 英语 |
88 |
82 |
94 |
85 |
76 |
85 |
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的标准差(要有过程).
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好!
如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为16厘米,要使两排挂钩之间 的距离为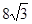 厘米,并在点B、M处固定,则B、M之间的距离是多少?
厘米,并在点B、M处固定,则B、M之间的距离是多少?