定义一种关于“⊙”的新运算,观察下列式子:
1⊙3=1×4+3=7;
3⊙(-1)=3×4+(-1)=11;
5⊙4=5×4+4=24;
4⊙(-3)=4×4+(-3)=13.
(1)请你想一想:5⊙(-6)= ;
(2)请你判断:当 时,a⊙b b⊙a(填入“=”或“≠”),并说明理由;
时,a⊙b b⊙a(填入“=”或“≠”),并说明理由;
如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.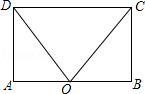
先化简,再求值:(x﹣2)(x+2)+x2(x﹣1),其中x=﹣1.
我市是世界有机蔬菜基地,数10种蔬菜在国际市场上颇具竞争力.某种有机蔬菜上市时,某经销商按市场价格10元/千克在我市收购了2000千克某种蔬菜存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨0.5元,但冷库存放这批蔬菜时每天需要支出各种费用合计340元,而且这种蔬菜在冷库中最多保存110天,同时,平均每天将会有6千克的蔬菜损坏不能出售.
(1)若存放x天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.
(2)经销商想获得利润22500元,需将这批蔬菜存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少?
如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.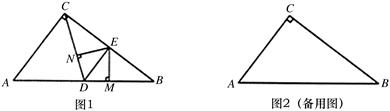
(1)当AD=CD时,求证DE∥AC;
(2)探究:AD为何值时,以B,M,E为顶点的三角形与以C,E,N为顶点的三角形相似?
某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.