已知向量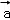 =(1,2),
=(1,2),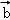 =(2,2).
=(2,2).
(1)求(2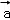 ﹣
﹣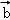 )•(2
)•(2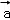 +
+ );
);
(2)设 =(﹣3,λ),若
=(﹣3,λ),若 与
与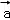 夹角为钝角,求λ的值.
夹角为钝角,求λ的值.
已知关于 的不等式
的不等式 的解集为
的解集为 .
.
(1)求实数 的值;
的值;
(2)解关于 的不等式:
的不等式: (
( 为常数).
为常数).
已知 的内角
的内角 所对边分别为
所对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求边长
,求边长 的最小值.
的最小值.
(本小题12分)已知函数 为奇函数,且在
为奇函数,且在 处取得极大值2.
处取得极大值2.
(1)求 的解析式;
的解析式;
(2)过点 (
( 可作函数
可作函数 图像的三条切线,求实数
图像的三条切线,求实数 的取值范围;
的取值范围;
(3)若 对于任意的
对于任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题12分)如图所示,在平面直角坐标系 中,过椭圆
中,过椭圆 内一点
内一点
 的一条直线与椭圆交于点
的一条直线与椭圆交于点 ,且
,且 ,其中
,其中 为常数.
为常数.
(1)求椭圆 的离心率;
的离心率;
(2)当点 恰为椭圆的右顶点时,试确定对应
恰为椭圆的右顶点时,试确定对应 的值;
的值;
(3)当 时,求直线
时,求直线 的斜率.
的斜率.
(本小题12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,其余人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,其余人主要的休闲方式是运动。
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系。
独立性检验观察值计算公式 ,
,
独立性检验临界值表:
 |
0.50 |
0.25 |
0.15 |
0.05 |
0.025 |
0.01 |
0.005 |
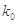 |
0.455 |
1.323 |
2.072 |
3.841 |
5.024 |
6.635 |
7.879 |