(本小题12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,其余人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,其余人主要的休闲方式是运动。
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系。
独立性检验观察值计算公式 ,
,
独立性检验临界值表:
 |
0.50 |
0.25 |
0.15 |
0.05 |
0.025 |
0.01 |
0.005 |
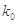 |
0.455 |
1.323 |
2.072 |
3.841 |
5.024 |
6.635 |
7.879 |
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求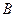 点在
点在 上,
上,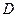 点在
点在 上,且对角线
上,且对角线 过
过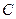 点,已知
点,已知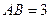 米,
米, 米.
米.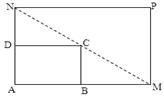
(I)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(II)当 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛 的面积最小?并求出最小值
的面积最小?并求出最小值
已知椭圆C中心在原点、焦点在 轴上,椭圆C上的点到焦点的最大值为
轴上,椭圆C上的点到焦点的最大值为 ,最小值为
,最小值为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线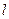 :
: 与椭圆交于不同的两点
与椭圆交于不同的两点 (
( 不是左、右顶点),且以
不是左、右顶点),且以 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点 .求证:直线
.求证:直线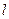 过定点,并求出定点的坐标
过定点,并求出定点的坐标
已知数列 的首项
的首项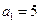 ,前
,前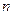 项和为
项和为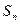 ,且
,且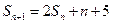
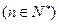 .
.
(Ⅰ)设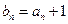 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前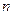 项和
项和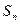 .
.
已知动圆过定点P(1,0),且与定直线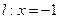 相切,点C在
相切,点C在 上.
上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-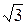 的直线与曲线M相交于A、B两点,
的直线与曲线M相交于A、B两点,
①求线段AB的长;
②问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线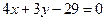 相切.
相切.
(1)求圆的方程;
(2)设直线 与圆相交于
与圆相交于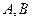 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?
?
存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.