某厂家拟在2011年举行促销活动，经调查测算，该产品的年销售量（即该厂的年产量）x万件与年促销费用m万元（m≥0）满足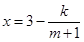
(k为常数)，如果不搞促销活动，则该产品的年销售量只能是1万件.已知2011年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍（产品成本包括固定投入和再投入两部分资金).
（Ⅰ）将2011年该产品的利润y万元表示为年促销费用m万元的函数；
（Ⅱ）该厂家2011年的促销费用投入多少万元时，厂家的利润最大.
。
的值和函数
的最小正周期；
的取值集合。
，集合
，求
；
B，求实数
的取值范围。
各项均为正数，
，且对于正整数
时，都有
。
，求
的值，并求数列
，存在与
，使得对于每个正整数
，都有
。
。
的单调区间；
成立，求实数
的取值范围。
。
时，解不等式
；
的最大值。