已知函数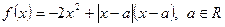 。
。
(I)当 时,解不等式
时,解不等式 ;
;
(II)求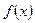 的最大值。
的最大值。
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表
| 班级 |
一 |
二 |
三 |
四 |
| 人数 |
3 |
2 |
3 |
4 |
(1)从这12人中随机抽取2人,求这2人恰好来自同一班级的概率.
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知函数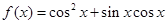 .
.
(1)求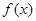 的最小正周期和最小值;
的最小正周期和最小值;
(2)若 且
且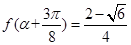 ,求
,求 的值.
的值.
已知函数 .
.
(1)试问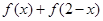 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;
(2)定义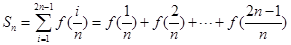 ,其中
,其中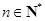 ,求
,求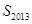 ;
;
(3)在(2)的条件下,令 .若不等式
.若不等式 对
对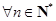 且
且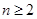 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知双曲线 经过点
经过点 ,且双曲线
,且双曲线 的渐近线与圆
的渐近线与圆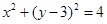 相切.
相切.
(1)求双曲线 的方程;
的方程;
(2)设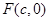 是双曲线
是双曲线 的右焦点,
的右焦点, 是双曲线
是双曲线 的右支上的任意一点,试判断以
的右支上的任意一点,试判断以 为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
已知数列{an}的前n项和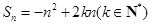 ,且
,且 的最大值为4.
的最大值为4.
(1)确定常数k的值,并求数列{an}的通项公式an;
(2)令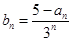 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与 的大小.
的大小.