已知函数f(x)=x2﹣2ax+a+2,
(1)若f(x)≤0的解集A⊆[0,3],求实数a的取值范围;
(2)若g(x)=f(x)+|x2﹣1|在区间(0,3)内有两个零点x1,x2(x1<x2),求实数a的取值范围.
已知集合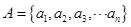 ,
,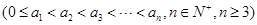
具有性质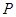 :对任意的
:对任意的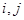
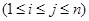 ,
,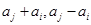 至少有一个属于
至少有一个属于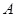 .
.
(1)分别判断集合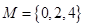 与
与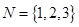 是否具有性质
是否具有性质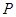 ;
;
(2)求证:①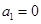 ;
;
②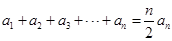 ;
;
(3)当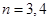 或
或 时集合
时集合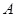 中的数列
中的数列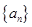 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.
已知椭圆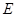 的两个焦点分别为
的两个焦点分别为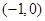 和
和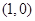 ,离心率
,离心率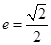 .
.
(1)求椭圆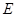 的方程;
的方程;
(2)设直线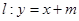 (
(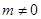 )与椭圆
)与椭圆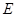 交于
交于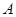 、
、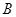 两点,线段
两点,线段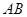 的垂直平分线交
的垂直平分线交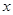 轴于点
轴于点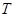 ,当
,当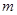 变化时,求
变化时,求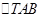 面积的最大值.
面积的最大值.
已知函数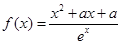 ,其
,其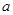 中为常数,
中为常数,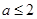 .
.
(1)当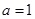 时,求曲线
时,求曲线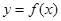 在点
在点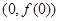 处的切线方程;
处的切线方程;
(2)是否存在实数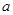 ,使
,使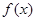 的极大值为
的极大值为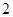 ?若存在,求出
?若存在,求出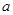 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图:在四棱锥 中,底面
中,底面 是正方形,
是正方形, ,
, ,点
,点 在
在 上,且
上,且 .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)证明:在线段 上存在点
上存在点 ,使
,使 ∥平面
∥平面 ,并求
,并求 的长.
的长.
甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于 分的次数为
分的次数为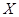 ,求
,求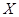 的分布列和数学期望
的分布列和数学期望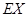 ..
..