下表是某小卖部6天卖出热茶的杯数与当天气温的对比表:
| 气温/℃ |
26 |
18 |
13 |
10 |
4 |
-1 |
| 杯数 |
20 |
24 |
34 |
38 |
50 |
64 |
(1)将上表中的数据制成散点图.
(2)你能从散点图中发现温度与饮料杯数近似成什么关系吗?
(3)如果近似成线性关系的话,请求出回归直线方程来近似地表示这种线性关系.
(4)如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
(本小题满分12分)
已知:如图,在四棱锥 中,四边形
中,四边形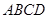 为正方形,
为正方形,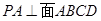 ,且
,且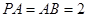 ,
, 为
为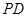 中点.
中点.
(1)证明: //平面
//平面 ;
;
(2)证明:平面 平面
平面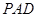 ;
;
(3)求二面角 的正弦值.
的正弦值.
(本小题满分12分)
已知各项均为正数的数列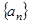 前
前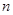 项和为
项和为 ,首项为
,首项为 ,且
,且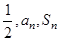 等差数列.
等差数列.
(1)求数列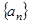 的通项公式;
的通项公式;
(2)若 ,设
,设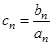 ,求数列
,求数列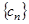 的前
的前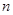 项和
项和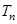 .
.
(本小题满分12分)
在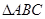 中,角
中,角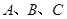 所对的边分别为
所对的边分别为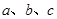 且
且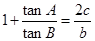 .
.
(1)求角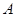 ;
;
(2)已知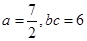 ,求
,求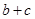 的值.
的值.
(本小题满分12分)
设命题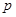 :实数
:实数 满足
满足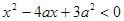 ,其中
,其中 ;命题
;命题 :实数
:实数 满足
满足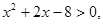 且
且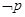 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知方程 .
.
(1)若此方程表示圆,求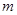 的取值范围;
的取值范围;
(2)若(1)中的圆与直线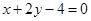 相交于
相交于 两点,且
两点,且 (
( 为坐标原点)求
为坐标原点)求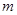 的值;
的值;
(3)在(2)的条件下,求以 为直径的圆的方程.
为直径的圆的方程.