如图所示,一电荷量q=3×10﹣4C带正电的小球,用绝缘细线悬于竖直放置足够大的平行金属板中的O点.电键S合上后,当小球静止时,细线与竖直方向的夹角α=37°.已知两板相距d=0.1m,电源电动势E=12V,内阻r=2Ω,电阻R1=4Ω,R2=R3=R4=12Ω.g取10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)通过电源的电流;
(2)两板间的电场强度的大小;
(3)小球的质量.
如图所示,一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g取10m/s2.试求:
(1)小球抛出点A距圆弧轨道B端的高度h.
(2)小球经过轨道最低点C时对轨道的压力FC.
(3)小球能否到达轨道最高点D?若能到达,试求对D点的压力FD.若不能到达,试说明理由.
2007年10月24日18时05分,中国第一颗探月卫星“嫦娥一号”在西昌卫星发射中心成功升空,“嫦娥奔月”成为中国航天的现实. 为了方便研究,我们将“嫦娥奔月”的过程简化为:“嫦娥一号”升空后,首先进入周期为T1的近地圆轨道,然后在地面的指令下经过一系列的变轨后最终被月球捕获,在距离月球表面为h的轨道上绕月球做匀速圆周运动. 已知地球质量为M1,半径为R1,月球质量为M2,半径为R2。求:“嫦娥一号”绕月球运动时的周期T2(最终结果用题目中的物理量来表示).
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力Fx垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止)。某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时,滑板做匀速直线运动,相应的k="54" kg/m,人和滑板的总质量为108 kg,试求(重力加速度g取10 m/s2,sin 37°=0.6,忽略空气阻力):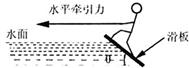
(1)水平牵引力的大小;
(2)滑板的速率;
如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg。试问:
①a与b球碰前瞬间的速度多大?
②a、b两球碰后,细绳是否会断裂?(要求通过计算回答)
以下两小题中任选一题做。
|
(1)如图所示是一列沿x轴正方向传播的简谐横波在t =0时刻的波形图,波的传播速度v = 2m/s,试求:
①x =" 4" m处质点的振动函数表达式