为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
| |
优秀 |
非优秀 |
总计 |
| 男生 |
40 |
20 |
60 |
| 女生 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
(Ⅰ)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为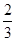 ,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量
,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量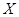 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求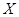 的分布列与数学期望.
的分布列与数学期望.
 |
0.500 |
0.400 |
0.100 |
0.010 |
0.001 |
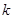 |
0.455 |
0.708 |
2.706 |
6.635 |
10.828 |
附: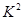 =
=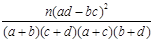
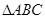 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量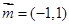 ,
,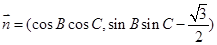 ,且
,且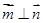 .
.
(Ⅰ)求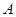 的大小;
的大小;
(Ⅱ)现在给出下列三个条件:1、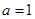 ;2、
;2、 ;3、
;3、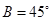 ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定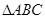 ,求出所确定的
,求出所确定的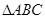 的面积.
的面积.
(注:只需要选择一种方案答题,如果用多种方案答题,则按第一方案给分).
已知函数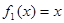 ,
,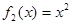 ,
,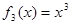 ,
,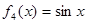 ,
,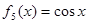 ,
, ,将它们分别写在六张卡片上,放在一个盒子中,
,将它们分别写在六张卡片上,放在一个盒子中,
(Ⅰ)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得的
函数是奇函数的概率;
(Ⅱ)从盒子中任取两张卡片,求其中至少一张上为奇函数的概率
已知函数 .
.
(Ⅰ)当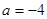 时,求
时,求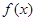 的最小值;
的最小值;
(Ⅱ)若函数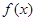 在区间
在区间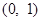 上为单调函数,求实数
上为单调函数,求实数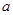 的取值范围;
的取值范围;
(Ⅲ)当 时,不等式
时,不等式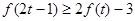 恒成立,求实数
恒成立,求实数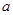 的取值范围.
的取值范围.
已知椭圆
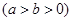 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线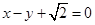 相切.
相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点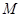 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足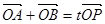 (
(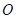 为坐标原点),当
为坐标原点),当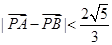 时,求实数
时,求实数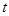 取值范围.
取值范围.
已知四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, .
.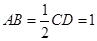 ,
, ,
,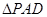 为正三角形,且面
为正三角形,且面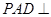 面
面 ,异面直线
,异面直线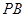 与
与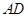 所成的角的余弦值为
所成的角的余弦值为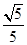 ,
,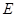 为
为 的中点.
的中点.
(Ⅰ)求证: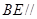 面
面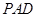 ;
;
(Ⅱ)求点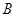 到平面
到平面 的距离;
的距离;
(Ⅲ)求平面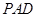 与平面
与平面 相交所成的锐二面角的大小.
相交所成的锐二面角的大小.